Princeton Algorithm 8 Puzzle–99分解答–java Python实现
完整代码及测试数据 完整代码及测试数据
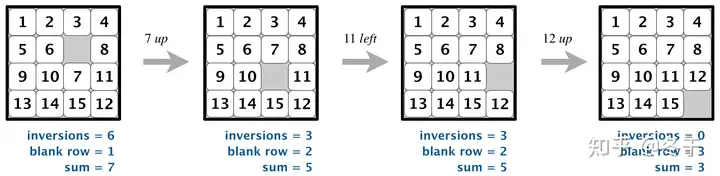
问题简介 八数码:是指在3x3的矩阵中,其中有8个格子放置成1-8,剩下一个格子是空格。能够移动和空格相邻的格子到空格,直到这个矩阵满足每一行依次从左到右读取是有序,得到最后得到1-8有序,最后一个格子是空格。下图展示了一个案例:
推广二维N×N的棋盘 对于任意大小的二维N×N的棋盘:
结论 先说结论:
一个状态表示成一维的形式,求出:除0之外 所有数字的逆序数之和,也就是每个数字前面比它大的数字的个数的和,称为这个状态的逆序。
若两个状态的逆序奇偶性相同,则可相互到达,否则不可相互到达。
N是奇数时,当且仅当当前棋盘的逆序对是偶数的时候有解。
N是偶数时,当且仅当当前棋盘的逆序对数加上空格所在的行(行数从0开始算)是奇数的时候有解。
证明
根据棋局的逆序对定义,不论N为奇数或偶数,空格在同一行的左右移动不会修改逆序对数的奇偶性 ;
不论N为奇数或偶数,空格上下移动,相当于跨过N-1个格子,那么逆序的改变可能为±N-1,±N-3,±N-5 …… ±N-2k-1。
此时,若N为偶数,空格上下移动,逆序对数的奇偶性必然改变 :比如N=4时,当上下移动的时候,相当于一个数字跨过了另外三个格子,它的逆序可能±3或±1。
若N为奇数,空格上下移动,逆序对数的奇偶性保持不变 :比如N=3时,当上下移动的时候,相当于一个数字跨过了另外三个格子,它的逆序可能±2或0。
所以:
当N为奇数时,空格上下左右移动都不改变奇偶性,当前棋盘的逆序对与目标状态逆序对的奇偶性相同时有解,当八数码问题中,目标状态的逆序对数为0(偶数),所以“N是奇数时,当且仅当当前棋盘的逆序对是偶数的时候有解”。
N为偶数时,空格每上下移动一次,奇偶性改变。称空格位置所在的行到目标空格所在的行步数为空格的距离 (不计左右距离),若两个状态的可相互到达,则有,两个状态的逆序奇偶性相同且空格距离为偶数,或者,逆序奇偶性不同且空格距离为奇数数 。否则不能。也就是说,当此表达式成立时,两个状态可相互到达:(状态1的逆序数 + 空格距离)的奇偶性==状态2奇偶性 。空格距离=N-空格所在行数 。
计算逆序对 可以利用归并排序时的“合并操作”来统计逆序对:
双指针i=0,j=0分别指向左半部分left和右半部分right的开始;
判断left[i]和right[j]的大小:
如果left[i]<=right[j],没有逆序对,i+=1;
如果left[i]>right[j],逆序对数为mid-i+1,j+=1;
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 def calInversionNumber (self ): nums=list (self.board_data.reshape(self.n*self.n)) for i in range (len (nums)): if nums[i]==0 : del nums[i] break tmp=nums.copy() def sortlist (l,r ): if l>=r:return 0 mid=l+(r-l)//2 res=sortlist(l, mid)+sortlist(mid+1 , r) if nums[mid]<nums[mid+1 ]:return res tmp[l:r+1 ]=nums[l:r+1 ] i,j=l,mid+1 for k in range (l,r+1 ): if i==mid+1 : nums[k]=tmp[j] j+=1 elif j==r+1 or tmp[i]<=tmp[j]: nums[k]=nums[i] i+=1 else : nums[k]=tmp[j] j+=1 res+=mid-i+1 return res res=sortlist(0 , len (nums)-1 ) if self.n&1 ==1 and res&1 ==0 : return True row,col=self.findzero() if self.n&1 ==0 and (res+row)&1 ==1 :return True return False
解法 广度优先遍历穷举:让空格不断和周围位置交换,直到换到棋局变成目标棋局。
A star启发式穷举:优先在队列中从有可能更快达到目标棋局的棋局继续穷举。
广度优先遍历(bfs) 让空格不断和周围位置交换,交换后的棋局加入队列,注意使用哈希集合防止遍历重复的棋局,广度优先遍历结束的树高就是步数。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 def solver_bfs (self ): step=0 queue=[self.board] dxdy=[[-1 ,0 ],[0 ,-1 ],[1 ,0 ],[0 ,1 ]] visited=set () visited.add(self.board.to_string()) n=self.board.n while queue: size=len (queue) for i in range (size): cur=queue.pop(0 ) if cur.is_solvable(): self.step=step self.ans_board=cur return row,col=cur.findzero() for dx,dy in dxdy: x,y=row+dx,col+dy if 0 <=x<n and 0 <=y<n: new_board=deepcopy(cur) self.swap(new_board.board_data,x,y,row,col) new_board.prev=cur new_str=new_board.to_string() if new_str not in visited: queue.append(new_board) visited.add(new_str) else : del new_board step+=1 return -1
A star(A*) A星算法是一种具备启发性策略的算法,优先在队列中从有可能更快达到目标棋局的棋局继续穷举。
更有可能达到目标棋局的当前棋局得分通过设置代价函数实现,为:已有的代价+未来的代价估计(可以使用曼哈顿、汉明距离等进行度量)。
所以只需要在计算当前棋局的代价,使用优先级队列,优先从代价较小的棋局继续穷举,就可能更快到达目标棋局。
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 def solver_astar (self ): queue=[] heapq.heappush(queue,self.board) dxdy=[[-1 ,0 ],[0 ,-1 ],[1 ,0 ],[0 ,1 ]] visited=set () visited.add(self.board.to_string()) n=self.board.n while queue: cur=heapq.heappop(queue) if cur.is_solvable(): self.ans_board=cur self.step=self.ans_board.height return row,col=cur.findzero() for dx,dy in dxdy: x,y=row+dx,col+dy if 0 <=x<n and 0 <=y<n: new_board=deepcopy(cur) self.swap(new_board.board_data,x,y,row,col) new_board.prev=cur new_str=new_board.to_string() new_board.height+=1 if new_str not in visited: heapq.heappush(queue,new_board) visited.add(new_str) else : del new_board self.ans_board=None return -1
参考资料 AlgorithmRunnig - 八数码 (qq.com)
Slider Puzzle Assignment (princeton.edu)
ZJU2004 Commedia dell’arte - 八数码问题有解的条件及其推广