强化学习--Reinforcement learning
强化学习
概念定义
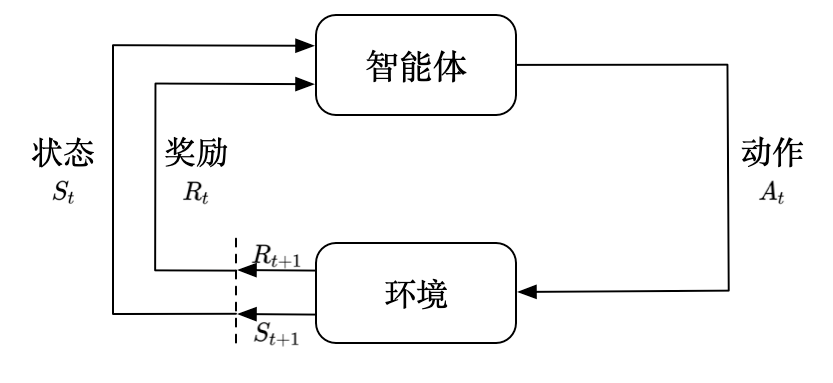
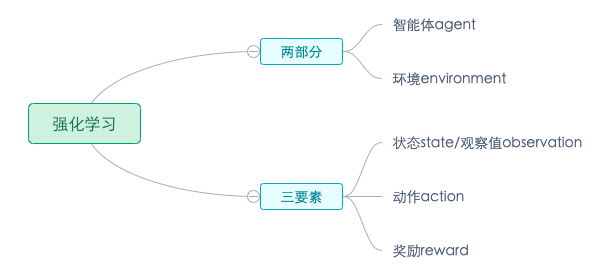
强化学习(Reinforcement learning,RL)讨论的问题是一个智能体(agent) 怎么在一个复杂不确定的 环境(environment) 里面去极大化它能获得的奖励。通过感知所处环境的 状态(state) 对 动作(action) 的 **反应(reward)**, 来指导更好的动作,从而获得最大的 **收益(return)**,这被称为在交互中学习,这样的学习方法就被称作强化学习。
Reinforcement learning is learning what to do—how to map situations to actions——so as to maximize a numerical reward signal.
—– Richard S. Sutton and Andrew G. Barto 《Reinforcement Learning: An Introduction II》
在强化学习过程中,智能体跟环境一直在交互。智能体在环境里面获取到状态,智能体会利用这个状态输出一个动作,一个决策。然后这个决策会放到环境之中去,环境会根据智能体采取的决策,输出下一个状态以及当前的这个决策得到的奖励。智能体的目的就是为了尽可能多地从环境中获取奖励。
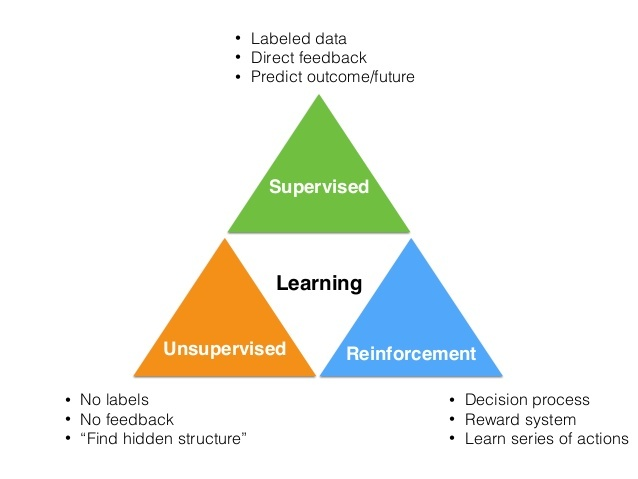
强化学习是除了监督学习和非监督学习之外的第三种基本的机器学习方法。
- 监督学习 是从外部监督者提供的带标注训练集中进行学习。 (任务驱动型)
- 非监督学习 是一个典型的寻找未标注数据中隐含结构的过程。 (数据驱动型)
- 强化学习 更偏重于智能体与环境的交互, 这带来了一个独有的挑战 ——“试错(exploration)”与“开发(exploitation)”之间的折中权衡,智能体必须开发已有的经验来获取收益,同时也要进行试探,使得未来可以获得更好的动作选择空间。 (从错误中学习)
强化学习主要有以下几个特点:
- 试错学习:强化学习一般没有直接的指导信息,Agent 要以不断与 Environment 进行交互,通过试错的方式来获得最佳策略(Policy)。
- 延迟回报:强化学习的指导信息很少,而且往往是在事后(最后一个状态(State))才给出的。比如 围棋中只有到了最后才能知道胜负。
基本元素
- 环境(Environment) 是一个外部系统,智能体处于这个系统中,能够感知到这个系统并且能够基于感知到的状态做出一定的行动。
- 智能体(Agent) 是一个嵌入到环境中的系统,能够通过采取行动来改变环境的状态。
- **状态(State)/观察值(Observation)**:状态是对世界的完整描述,不会隐藏世界的信息。观测是对状态的部分描述,可能会遗漏一些信息。
- **动作(Action)**:不同的环境允许不同种类的动作,在给定的环境中,有效动作的集合经常被称为动作空间(action space),包括离散动作空间(discrete action spaces)和连续动作空间(continuous action spaces),例如,走迷宫机器人如果只有东南西北这 4 种移动方式,则其为离散动作空间;如果机器人向 360◦ 中的任意角度都可以移动,则为连续动作空间。
- **奖励(Reward)**:是由环境给的一个标量的反馈信号(scalar feedback signal),这个信号显示了智能体在某一步采 取了某个策略的表现如何。
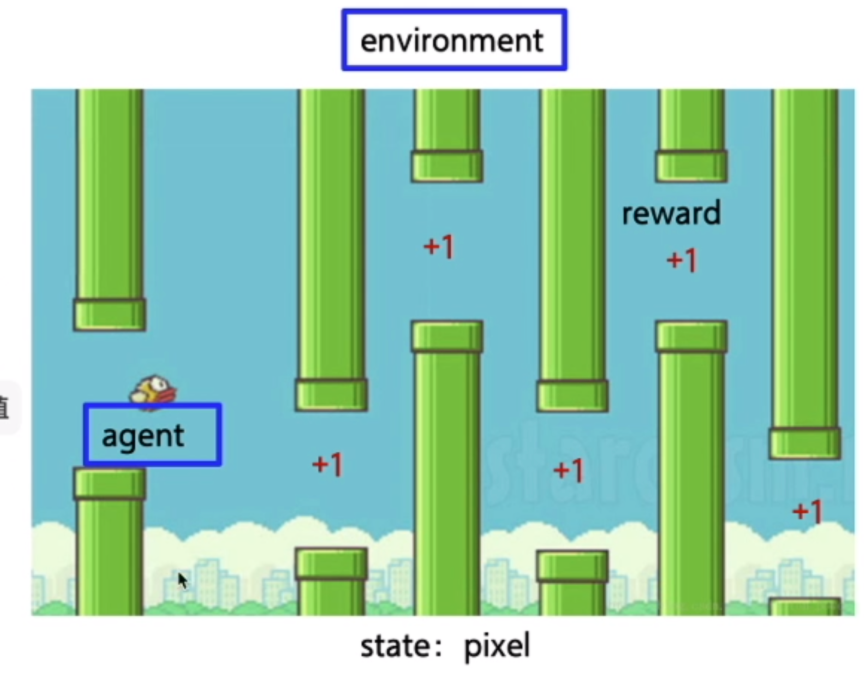
| 名称 | 对应上图中的内容 |
|---|---|
| agent | 鸟 |
| environment | 鸟周围的环境,水管、天空(包括小鸟本身) |
| state | 拍个照(目前的像素) |
| action | 向上向下动作 |
| reward | 距离(越远奖励越高) |
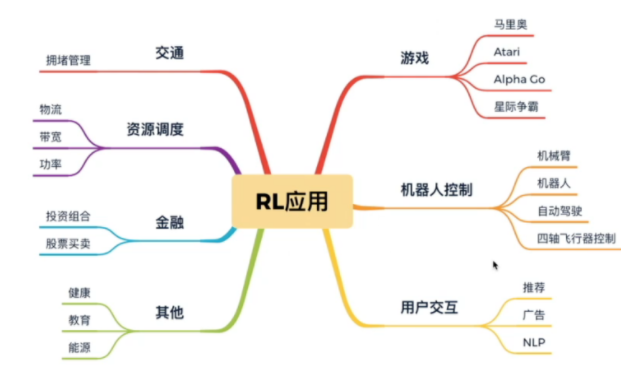
应用场景
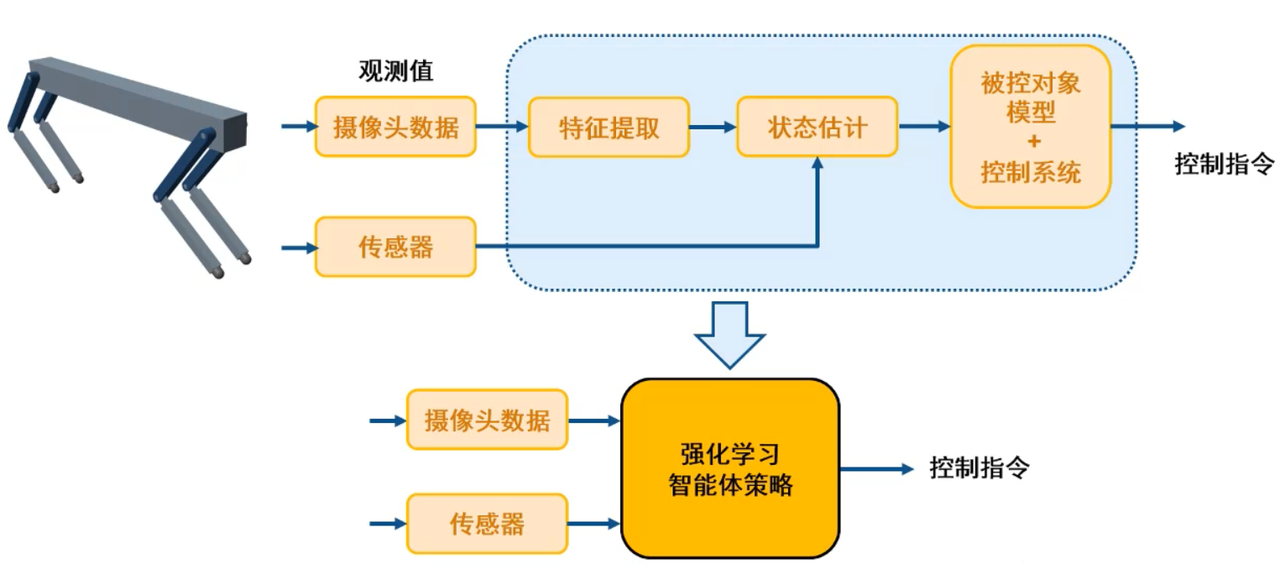
| 名称 | 对应上图中的内容 |
|---|---|
| agent | 策略-保持机器人平衡并行走 |
| environment | 机器人、地面、外部干扰 |
| state | 传感器采集的信号 |
| action | 作用在机器人各个关节的电机扭矩 |
| reward | 评估控制性能的数值信号 |
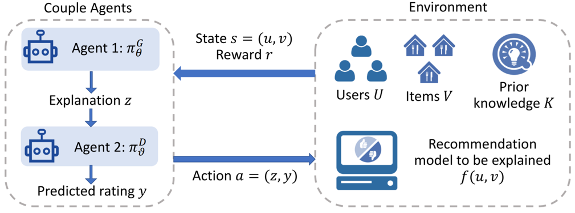
A Reinforcement Learning Framework for Explainable Recommendation
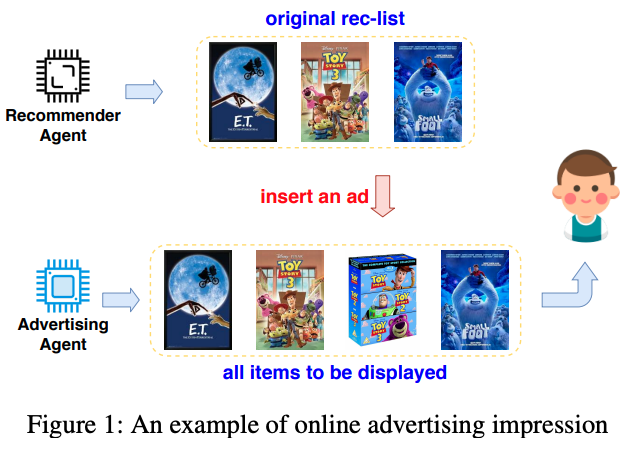
Deep Reinforcement Learning for Online Advertising in Recommender Systems.
同时解决三个任务:是否插入广告;如果插入,插入哪一条广告;以及插入广告在推荐列表的哪个位置。
相关术语
策略(Policy)
策略是智能体用于决定下一步执行什么行动的规则。可以是确定性的,一般表示为:�μ:
��=�(��)at=μ(st)
也可以是随机的,一般表示为 �π:
��∼�(⋅∣��)at∼π(⋅∣st)
状态转移(State Transition)
状态转移,可以是确定的也可以是随机的,一般认为是随机的,其随机性来源于环境。可以用状态密度函数来表示:
�(�′∣�,�)=�(�′=�′∣�=�,�=�)p(s′∣s,a)=P(S′=s′∣S=s,A=a)
环境可能会变化,在当前环境和行动下,衡量系统状态向某一个状态转移的概率是多少,注意环境的变化通常是未知的。
回报(Return)
回报又称cumulated future reward,一般表示为�U,定义为
��=��+��+1+��+2+��+3+⋯Ut=Rt+Rt+1+Rt+2+Rt+3+⋯
其中��Rt表示第t时刻的奖励,agent的目标就是让Return最大化。
未来的奖励不如现在等值的奖励那么好(比如一年后给100块不如现在就给),所以��+1Rt+1的权重应该小于��Rt。因此,强化学习通常用discounted return(折扣回报,又称cumulative discounted future reward),取�γ为discount rate(折扣率),�∈(0,1]γ∈(0,1],则有,
��=��+���+1+�2��+2+�3��+3+⋯Ut=Rt+γRt+1+γ2Rt+2+γ3Rt+3+⋯
价值函数(Value Function)
举例来说,在象棋游戏中,定义赢得游戏得1分,其他动作得0分,状态是棋盘上棋子的位置。仅从1分和0分这两个数值并不能知道智能体在游戏过程中到底下得怎么样,而通过价值函数则可以获得更多洞察。
价值函数使用期望对未来的收益进行预测,一方面不必等待未来的收益实际发生就可以获知当前状态的好坏,另一方面通过期望汇总了未来各种可能的收益情况。使用价值函数可以很方便地评价不同策略的好坏。
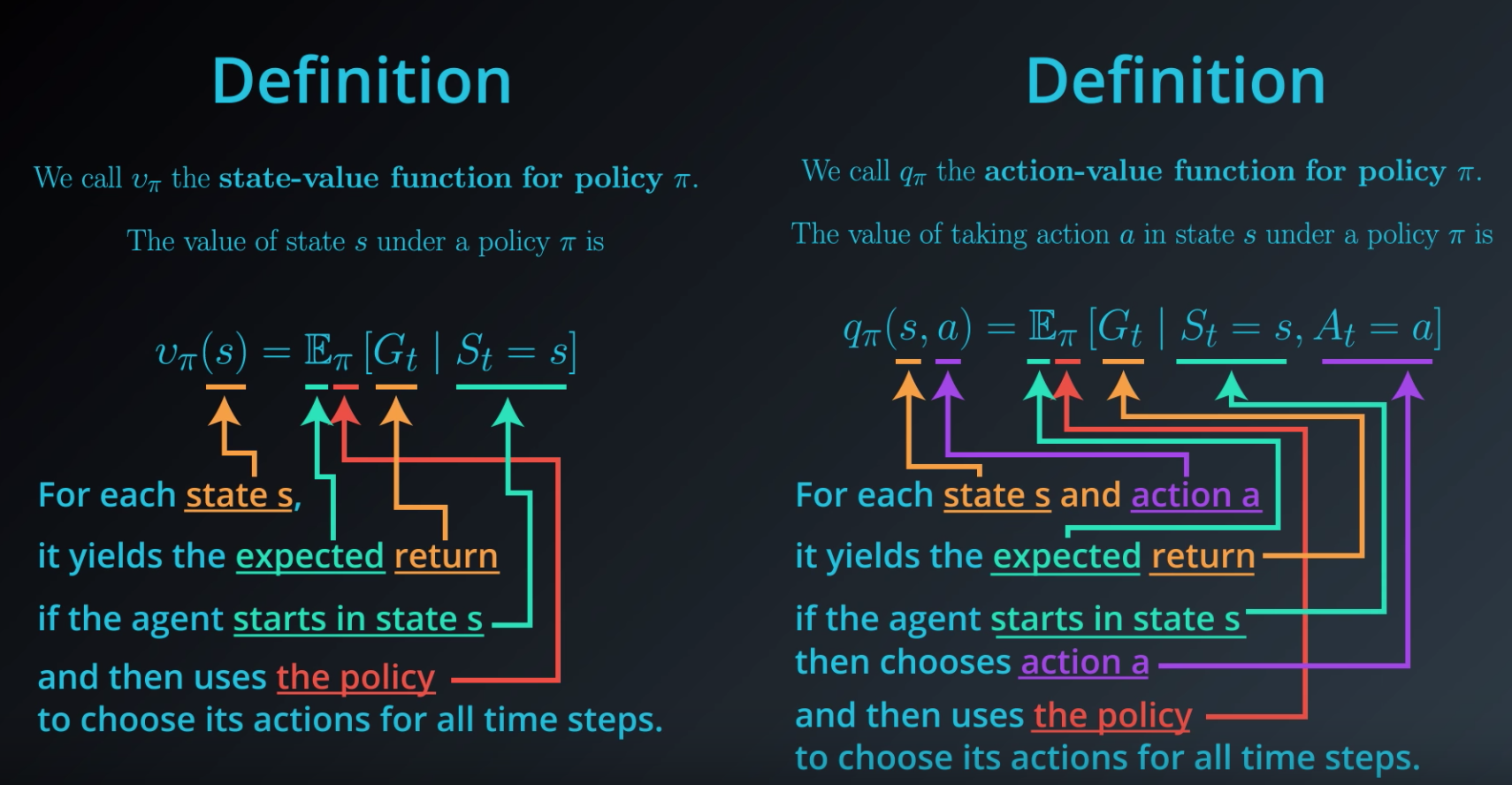
- 状态价值函数(State-value Function):用来度量给定策略�π的情况下,当前状态��st的好坏程度。
- 动作价值函数(Action-value Function):用来度量给定状态��st和策略�π的情况下,采用动作��at的好坏程度。
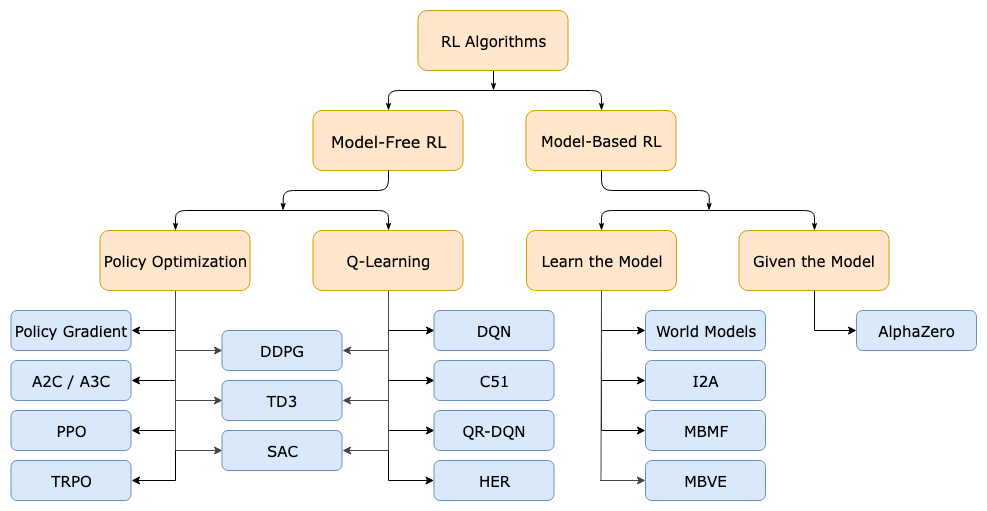
算法分类
按照环境是否已知划分:免模型学习(Model-Free) vs 有模型学习(Model-Based)
- Model-free就是不去学习和理解环境,环境给出什么信息就是什么信息,常见的方法有policy optimization和Q-learning。
- Model-Based是去学习和理解环境,学会用一个模型来模拟环境,通过模拟的环境来得到反馈。Model-Based相当于比Model-Free多了模拟环境这个环节,通过模拟环境预判接下来会发生的所有情况,然后选择最佳的情况。
一般情况下,环境都是不可知的,所以这里主要研究无模型问题。
按照学习方式划分:在线策略(On-Policy) vs 离线策略(Off-Policy)
- On-Policy是指agent必须本人在场, 并且一定是本人边玩边学习。典型的算法为Sarsa。
- Off-Policy是指agent可以选择自己玩, 也可以选择看着别人玩, 通过看别人玩来学习别人的行为准则, 离线学习同样是从过往的经验中学习, 但是这些过往的经历没必要是自己的经历, 任何人的经历都能被学习,也没有必要是边玩边学习,玩和学习的时间可以不同步。典型的方法是Q-learning,以及Deep-Q-Network。
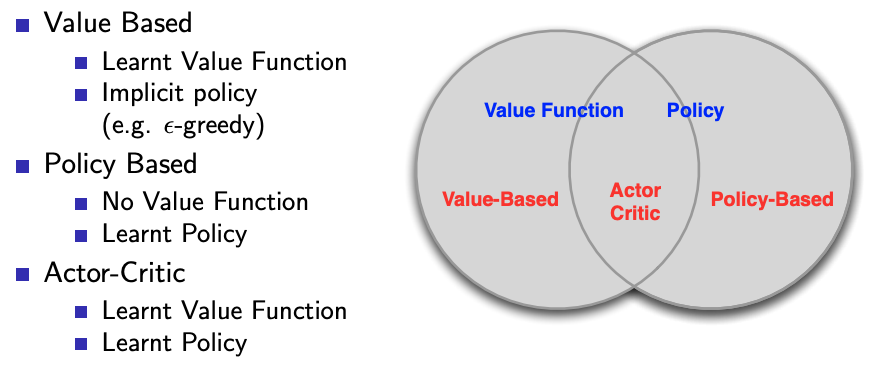
按照学习目标划分:基于策略(Policy-Based)和基于价值(Value-Based)。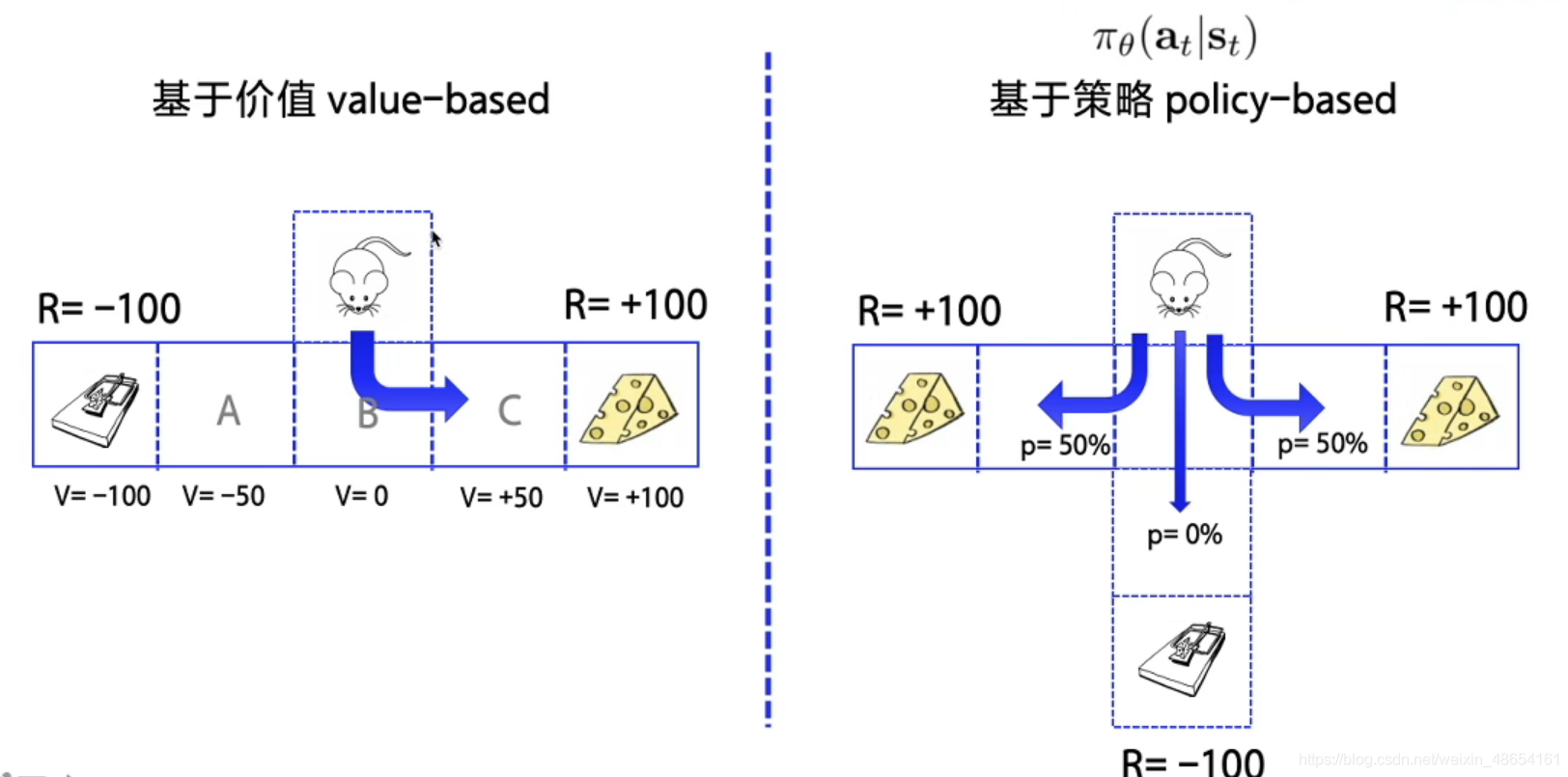
- Policy-Based的方法直接输出下一步动作的概率,根据概率来选取动作。但不一定概率最高就会选择该动作,还是会从整体进行考虑。适用于非连续和连续的动作。常见的方法有Policy gradients。
- Value-Based的方法输出的是动作的价值,选择价值最高的动作。适用于非连续的动作。常见的方法有Q-learning、Deep Q Network和Sarsa。
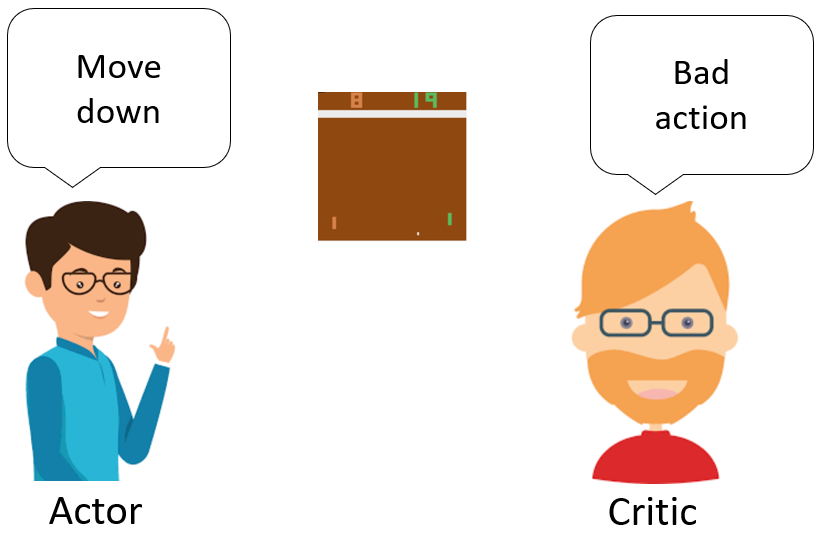
- 更为厉害的方法是二者的结合:Actor-Critic,Actor根据概率做出动作,Critic根据动作给出价值,从而加速学习过程,常见的有A2C,A3C,DDPG等。
经典算法
经典算法:Q-learning,Sarsa,DQN,Policy Gradient,A3C,DDPG,PPO
| 学习方法 | 说明 | 经典算法 |
|---|---|---|
| 基于价值(Value-Based) | 通过价值选行为 | Q Learning, Sarsa, Deep Q Network |
| 基于策略(Policy-Based) | 直接选最佳行为 | Policy Gradients |
| 基于模型(Model-Based) | 想象环境并从中学习 | Model based RL |
Value-Based & Policy-Based & Actor Critic
下面我们挑选一些有代表性的算法进行讲解:
- 基于表格、没有神经网络参与的Q-Learning算法
- 基于价值(Value-Based)的Deep Q Network(DQN)算法
- 基于策略(Policy-Based)的Policy Gradient(PG)算法
- 结合了Value-Based和Policy-Based的Actor Critic算法。
Q-Learning
在Q-learning中,我们维护一张Q值表,表的维数为:状态数S * 动作数A,表中每个数代表在当前状态S下可以采用动作A可以获得的未来收益的折现和。我们不断的迭代我们的Q值表使其最终收敛,然后根据Q值表我们就可以在每个状态下选取一个最优策略。
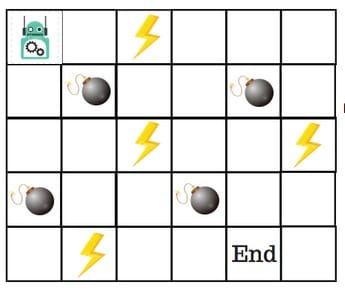
假设机器人必须越过迷宫并到达终点。有地雷,机器人一次只能移动一个地砖。如果机器人踏上矿井,机器人就死了。机器人必须在尽可能短的时间内到达终点。
得分/奖励系统如下:
- 机器人在每一步都失去1点。这样做是为了使机器人采用最短路径并尽可能快地到达目标。
- 如果机器人踩到地雷,则点损失为100并且游戏结束。
- 如果机器人获得动力⚡️,它会获得1点。
- 如果机器人达到最终目标,则机器人获得100分。
现在,显而易见的问题是:我们如何训练机器人以最短的路径到达最终目标而不踩矿井?
Q值表
Q值表(Q-Table)是一个简单查找表的名称,我们计算每个状态的最大预期未来奖励。基本上,这张表将指导我们在每个状态采取最佳行动。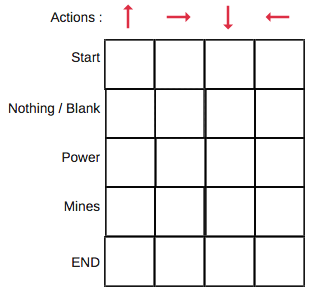
Q函数
Q函数(Q-Function)即为上文提到的动作价值函数,他有两个输入:「状态」和「动作」。它将返回在该状态下执行该动作的未来奖励期望。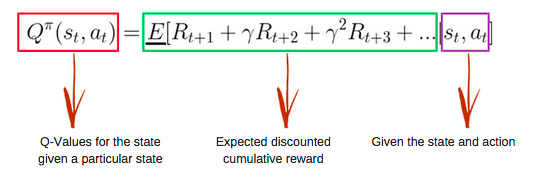
我们可以把Q函数视为一个在Q-Table上滚动的读取器,用于寻找与当前状态关联的行以及与动作关联的列。它会从相匹配的单元格中返回 Q 值。这就是未来奖励的期望。
在我们探索环境(environment)之前,Q-table 会给出相同的任意的设定值(大多数情况下是 0)。随着对环境的持续探索,这个 Q-table 会通过迭代地使用 Bellman 方程(动态规划方程)更新 Q(s,a) 来给出越来越好的近似。
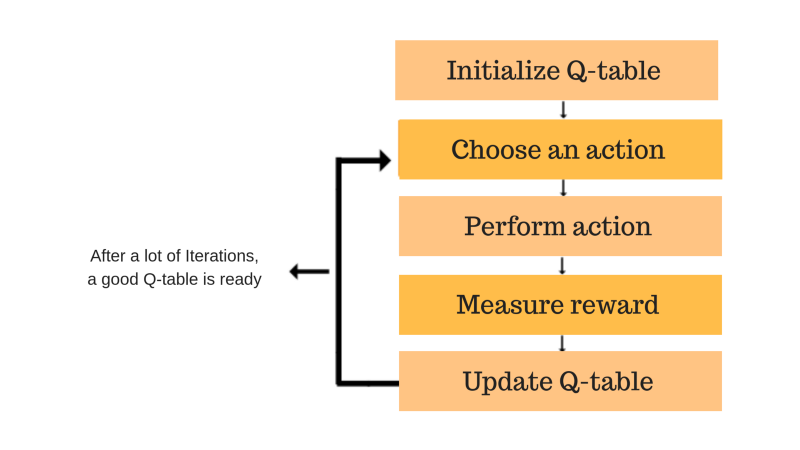
算法流程
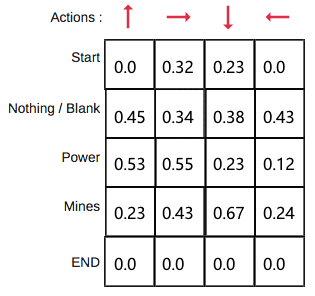
第1步:初始化Q值表
我们将首先构建一个Q值表。有n列,其中n=操作数。有m行,其中m=状态数。我们将值初始化为0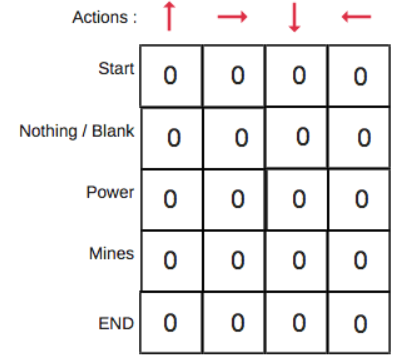
步骤2和3:选择并执行操作
这些步骤的组合在不确定的时间内完成。这意味着此步骤一直运行,直到我们停止训练,或者训练循环停止。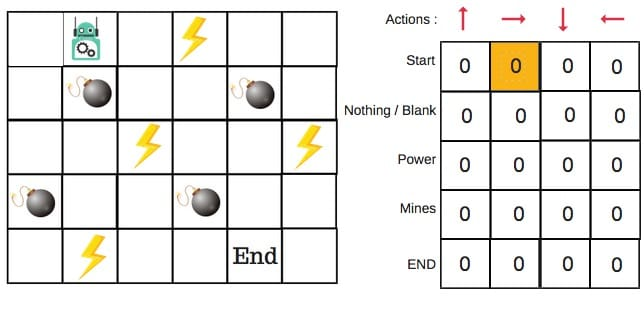
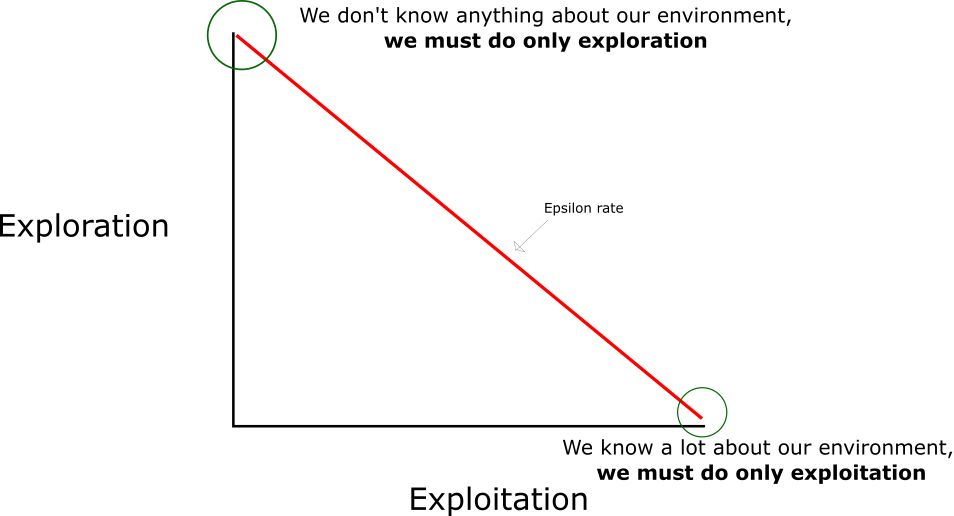
如果每个Q值都等于零,我们就需要权衡探索/利用(exploration/exploitation)的程度了,思路就是,在一开始,我们将使用 epsilon 贪婪策略:
- 我们指定一个探索速率「epsilon」,一开始将它设定为 1。这个就是我们将随机采用的步长。在一开始,这个速率应该处于最大值,因为我们不知道 Q-table 中任何的值。这意味着,我们需要通过随机选择动作进行大量的探索。
- 生成一个随机数。如果这个数大于 epsilon,那么我们将会进行「利用」(这意味着我们在每一步利用已经知道的信息选择动作)。否则,我们将继续进行探索。
- 在刚开始训练 Q 函数时,我们必须有一个大的 epsilon。随着智能体对估算出的 Q 值更有把握,我们将逐渐减小 epsilon。
步骤4和5:评估
现在我们采取了行动并观察了结果和奖励。我们需要更新功能Q(s,a):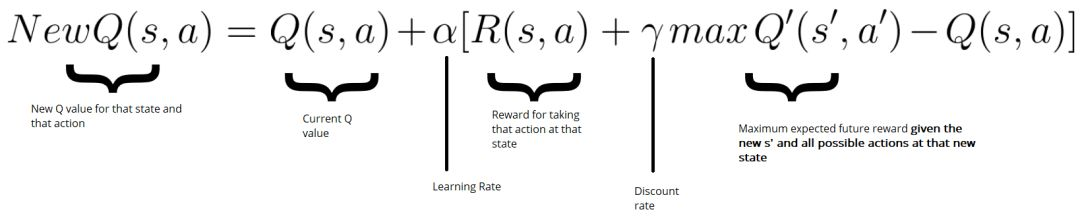
Deep Q Network
在普通的Q-learning中,当状态和动作空间是离散且维数不高时可使用Q-Table储存每个状态动作对的Q值,而当状态和动作空间是高维连续时,使用Q-Table不现实,我们无法构建可以存储超大状态空间的Q_table。不过,在机器学习中, 有一种方法对这种事情很在行,那就是神经网络,可以将状态和动作当成神经网络的输入,然后经过神经网络分析后得到动作的 Q 值,这样就没必要在表格中记录 Q 值,而是直接使用神经网络预测Q值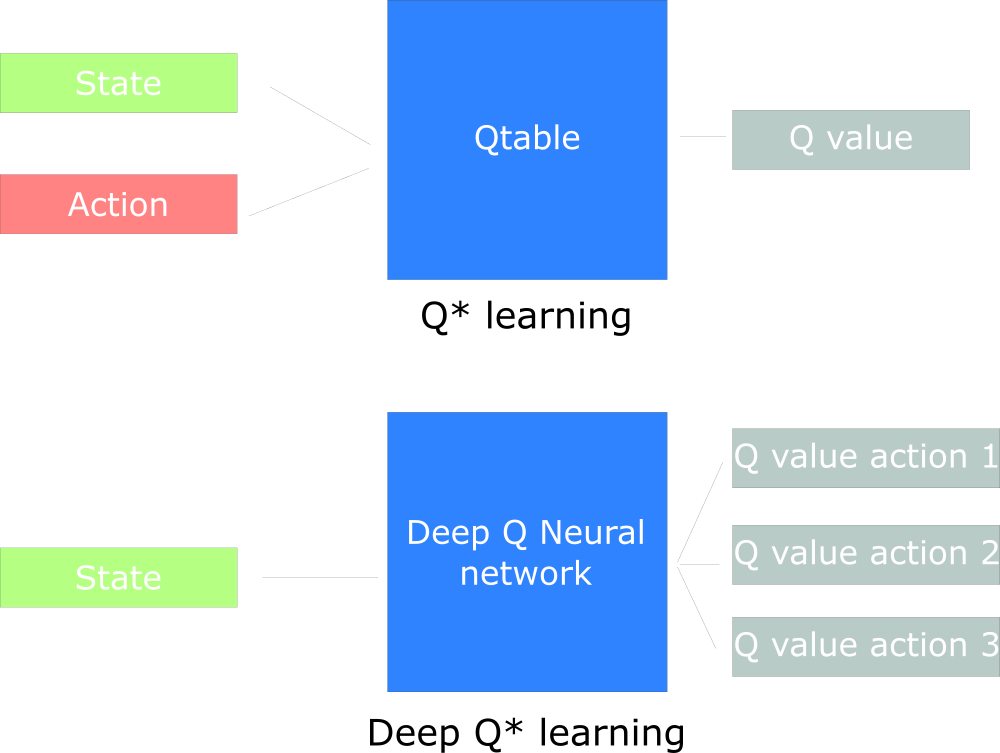
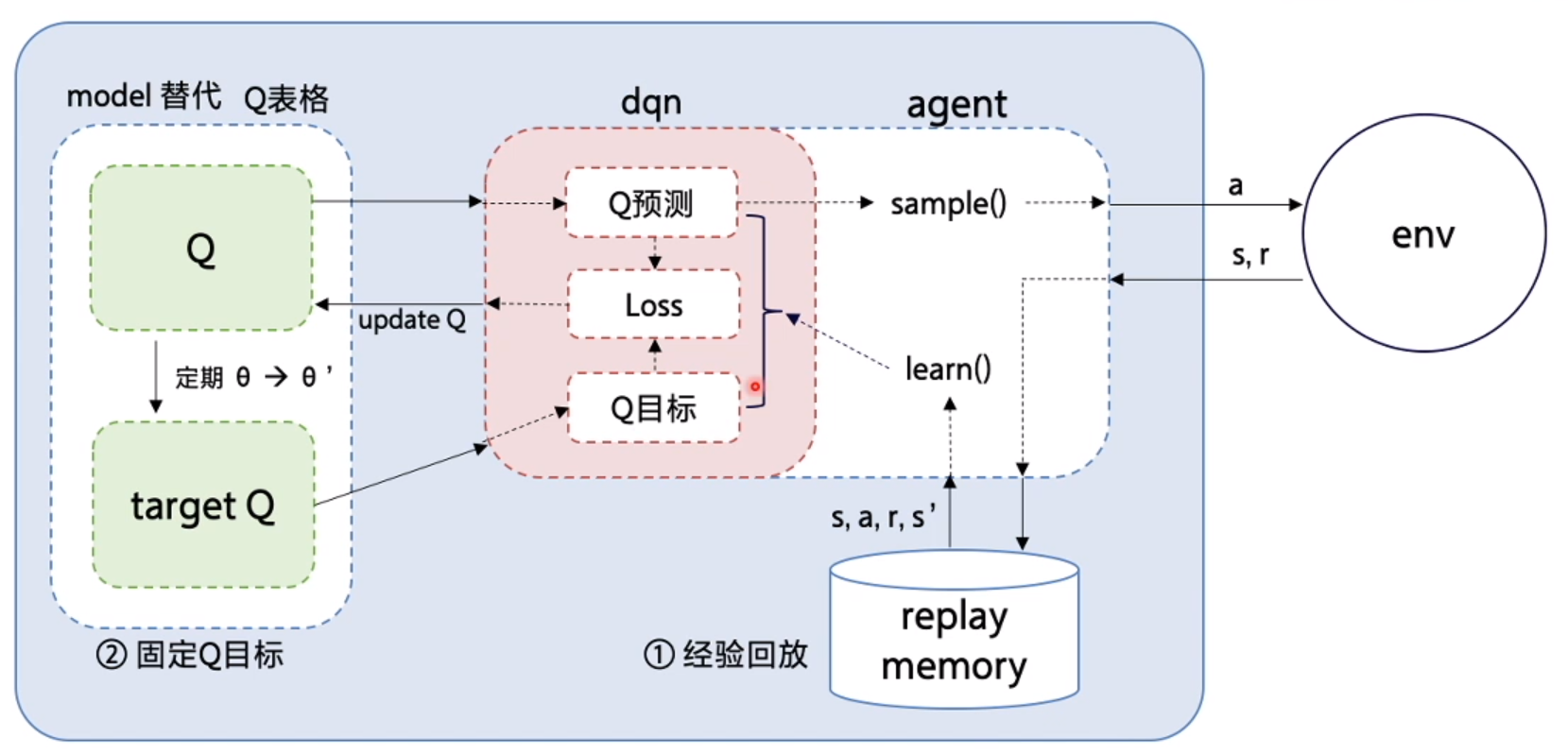
经验回放
DQN利用Qlearning特点,目标策略与动作策略分离,学习时利用经验池储存的经验取batch更新Q。同时提高了样本的利用率,也打乱了样本状态相关性使其符合神经网络的使用特点。
固定Q目标
神经网络一般学习的是固定的目标,而Qlearning中Q同样为学习的变化量,变动太大不利于学习。所以DQN使Q在一段时间内保持不变,使神经网络更易于学习。
算法流程
主要问题
- 在估计值函数的时候一个任意小的变化可能导致对应动作被选择或者不被选择,这种不连续的变化是致使基于值函数的方法无法得到收敛保证的重要因素。
- 选择最大的Q值这样一个搜索过程在高纬度或者连续空间是非常困难的;
- 无法学习到随机策略,有些情况下随机策略往往是最优策略。
Policy Gradient
前面我们介绍的Q-Learning和DQN都是基于价值的强化学习算法,在给定一个状态下,计算采取每个动作的价值,我们选择有最高Q值(在所有状态下最大的期望奖励)的行动。如果我们省略中间的步骤,即直接根据当前的状态来选择动作,也就引出了强化学习中的另一种很重要的算法,即策略梯度(Policy Gradient, PG)
策略梯度不通过误差反向传播,它通过观测信息选出一个行为直接进行反向传播,当然出人意料的是他并没有误差,而是利用reward奖励直接对选择行为的可能性进行增强和减弱,好的行为会被增加下一次被选中的概率,不好的行为会被减弱下次被选中的概率。
举例如下图所示:输入当前的状态,输出action的概率分布,选择概率最大的一个action作为要执行的操作。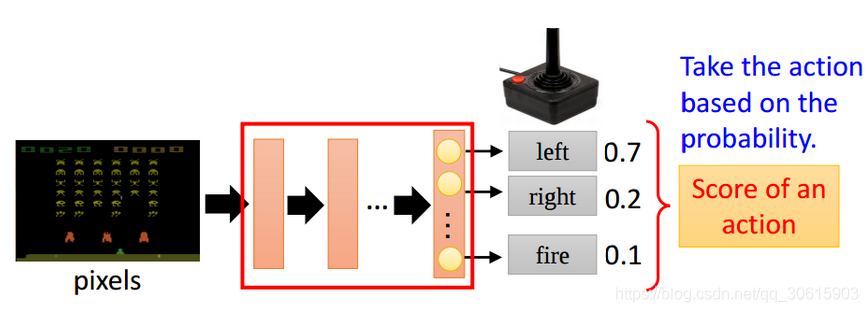
优缺点
优点
- 连续的动作空间(或者高维空间)中更加高效;
- 可以实现随机化的策略;
- 某种情况下,价值函数可能比较难以计算,而策略函数较容易。
缺点
- 通常收敛到局部最优而非全局最优
- 评估一个策略通常低效(这个过程可能慢,但是具有更高的可变性,其中也会出现很多并不有效的尝试,而且方差高)
REINFORCE
蒙特卡罗策略梯度reinforce算法是策略梯度最简单的也是最经典的一个算法。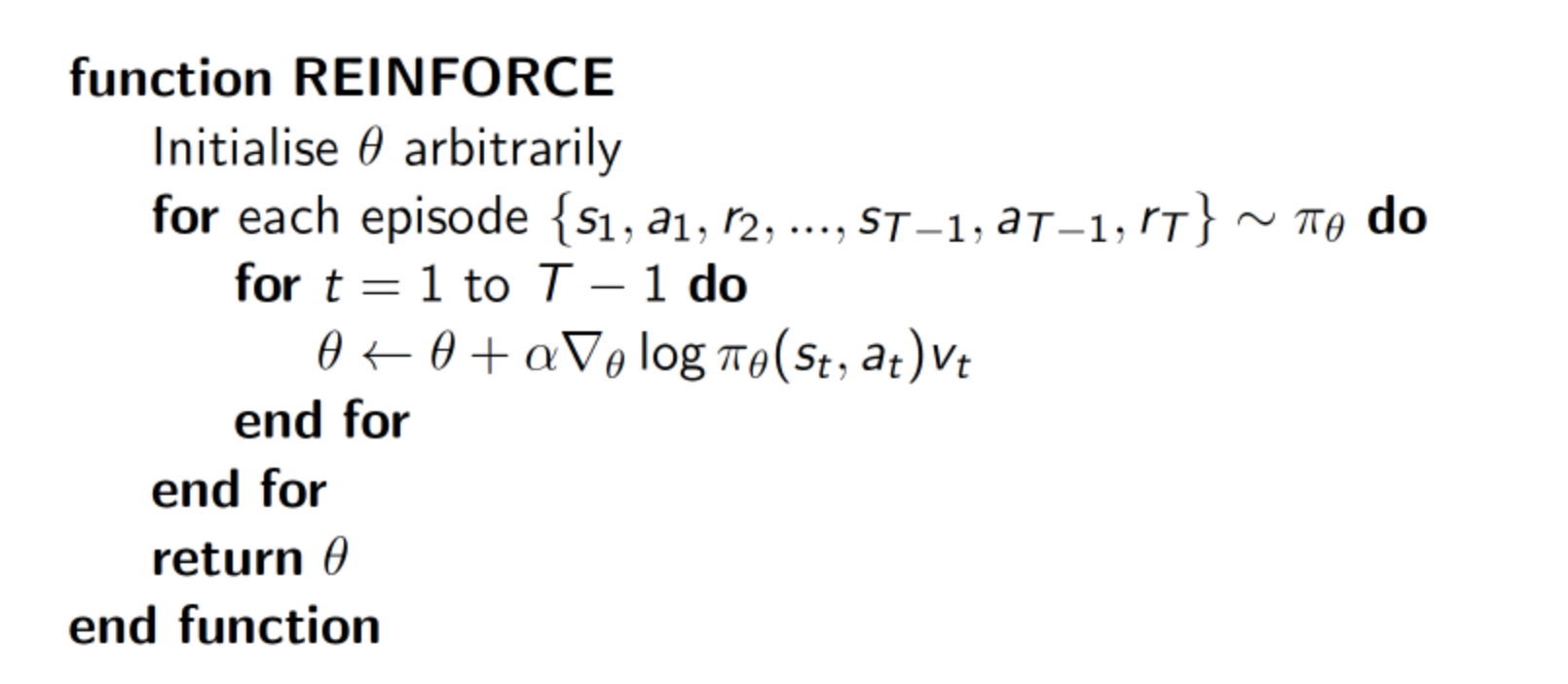
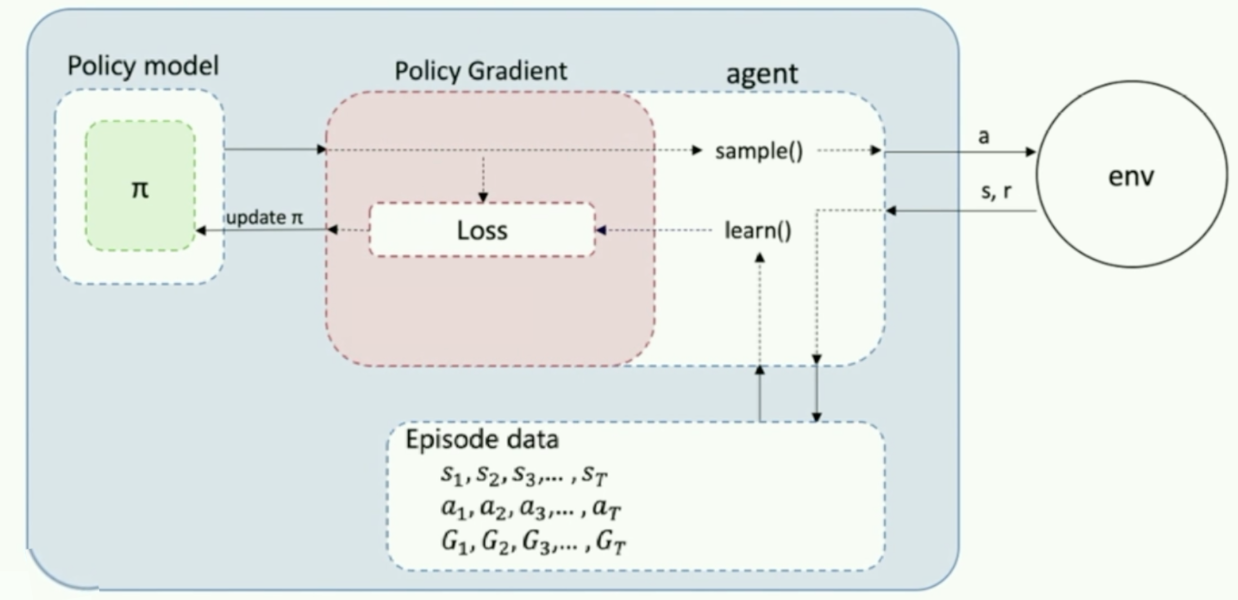
算法流程
首先我们需要一个 policy model 来输出动作概率,输出动作概率后,我们 sample() 函数去得到一个具体的动作,然后跟环境交互过后,我们可以得到一整个回合的数据。拿到回合数据之后,我再去执行一下 learn() 函数,在 learn() 函数里面,我就可以拿这些数据去构造损失函数,扔给这个优化器去优化,去更新我的 policy model。
Actor Critic
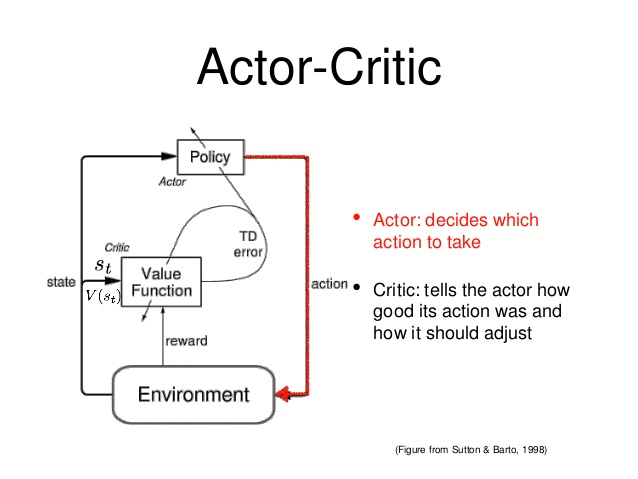
演员-评论家算法(Actor-Critic)是基于策略(Policy Based)和基于价值(Value Based)相结合的方法
- 演员(Actor)是指策略函数 ��(�∣�)πθ(a∣s),即学习一个策略来得到尽量高的回报。
- 评论家(Critic)是指值函数 ��(�)Vπ(s),对当前策略的值函数进行估计,即评估演员的好坏。
- 借助于价值函数,演员-评论家算法可以进行单步更新参数,不需要等到回合结束才进行更新。
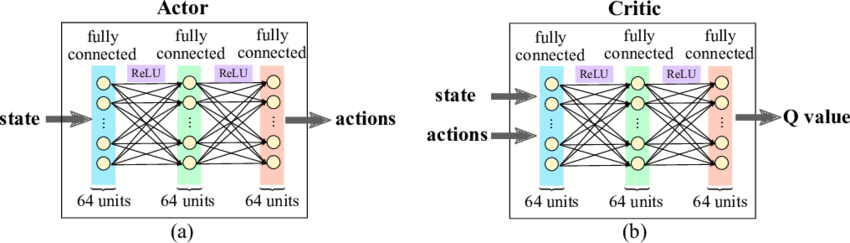
网络结构
算法流程
问题和改进
Actor Critic 取决于 Critic 的价值判断, 但是 Critic 难收敛, 再加上 Actor 的更新, 就更难收敛,为了解决该问题又提出了 A3C 算法和 DDPG 算法。
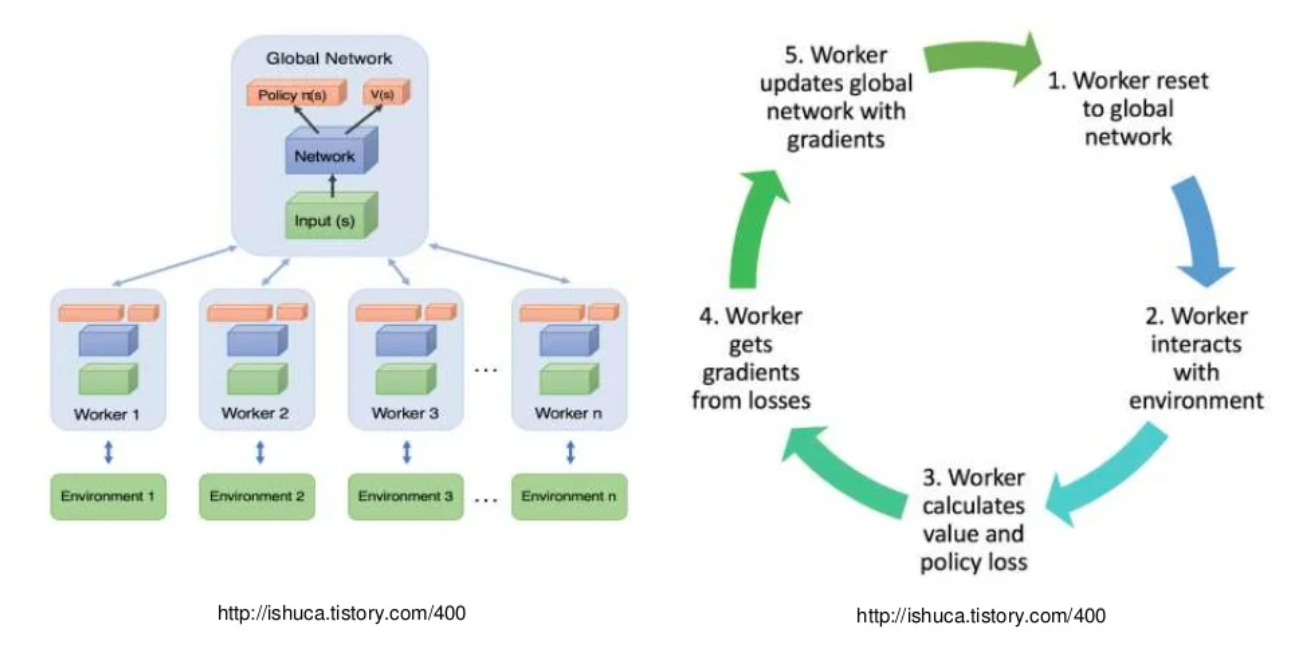
改进算法1:A3C
异步的优势行动者评论家算法(Asynchronous Advantage Actor-Critic,A3C),相比Actor-Critic,A3C的优化主要有3点,分别是异步训练框架,网络结构优化,Critic评估点的优化。其中异步训练框架是最大的优化。
改进算法2:DDPG
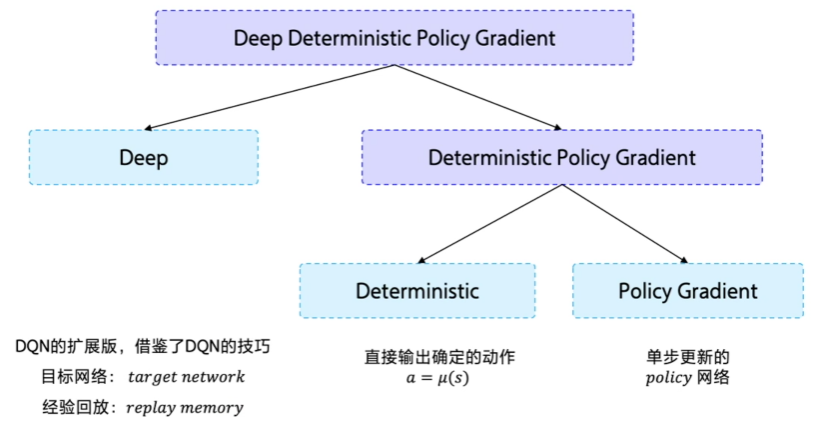
深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG),从DDPG这个名字看,它是由D(Deep)+D(Deterministic )+ PG(Policy Gradient)组成。
- Deep 是因为用了神经网络;
- Deterministic 表示 DDPG 输出的是一个确定性的动作,可以用于连续动作的一个环境;
- Policy Gradient 代表的是它用到的是策略网络。REINFORCE 算法每隔一个 episode 就更新一次,但 DDPG 网络是每个 step 都会更新一次 policy 网络,也就是说它是一个单步更新的 policy 网络。
参考资料
- 强化学习介绍 / OpenAI Spinning Up
- EasyRL / datawhalechina
- 0084. 强化学习(19) / 刘建平Pinard / cnblogs
- Deep Reinforcement Learning / wangshusen
- 强化学习Reinforcement Learning / 莫烦Python
- UCL Course on RL / David Silver / 2015
- Playing Atari with Deep Reinforcement Learning / David Silver / 2013
- Human-level control through deep reinforcement learning / David Silver / 2015
- 一图看懂DQN(Deep Q-Network)深度强化学习算法 / 薄荷-塘
- Policy gradient methods for reinforcement learning with function approximation.
- 强化学习——策略梯度与Actor-Critic算法 / 野风 / 知乎
- Asynchronous Methods for Deep Reinforcement Learning / Google DeepMind / A3C

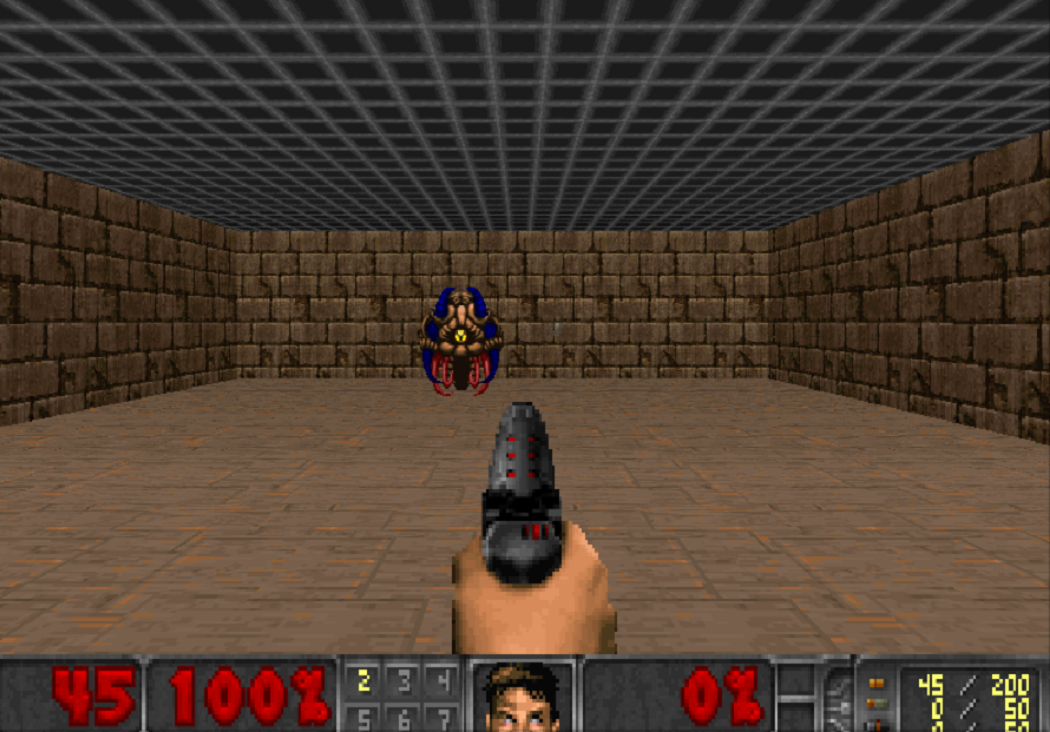
 强化学习游戏领域的应用
强化学习游戏领域的应用